Fabrizio Antenucci, Florent Krzakala, Pierfrancesco Urbani, Lenka Zdeborová
A generic inference problem can be described in the following way: given a set of measurements (that can be noisy or even non linear), how can we reconstruct the original signal from which they come from? What is the reconstruction error? Which kind of algorithms can we use? These questions can be addressed in simple generative models in which one generates a set of artificial data from a given signal through a known process (the teacher) and play the inference game (which is assigned to a student). This is a probabilistic setting that naturally brings to disordered statistical physics models.
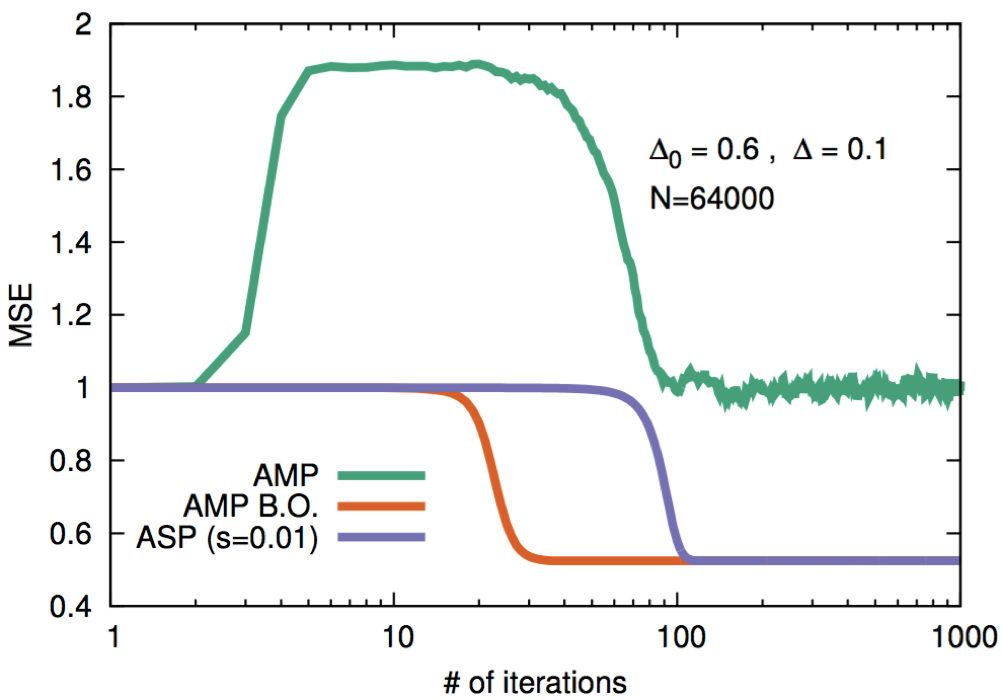
In the last work we have analyzed what happens when, in the inference game, the information about the statistical nature of the generative models is not used properly. In this case the student does not know perfectly the probabilistic informations about the teacher and we have shown that the reconstruction ability of a simple algorithm, called Approximate Message Passing (AMP), is degraded. This is due to glassiness in the statistical distribution (the posterior) over the signal. Therefore we have introduced a new algorithm, that we have called Approximate Survey Propagation (ASP) that extends AMP to include glassy effects. We have shown that this algorithm perform much better than AMP. This is shown in the figure where we plot the Mean Squared Error (MSE) between the reconstructed signal (through the two different algorithms) and the true one. The orange line represents the MSE that can be achieved when the student uses properly the information on the teacher.
Fabrizio Antenucci, Florent Krzakala, Pierfrancesco Urbani, Lenka Zdeborová, Approximate Survey Propagation for Statistical Inference, J. Stat. Mech. (2019) arXiv:1807.01296
Résultats obtenus dans le cadre du projet StatPhysDisSys financépar le thème 2 du LabEx PALM et portépar Pierfrancesco Urbani (IPhT)