F. Antenucci (CEA), P. Urbani (CEA), F. Krzakala (ENS), S. Franz (LPTMS), L. Zdeborová (CEA)
Learning of representations of data stands behind the recent progress in machine learning and paves our way towards artificial intelligence. Certain models for representation learning can be seen as a particular kind of a mean-field spin glasses. Methods stemming from physics of disordered systems turn out as very instrumental in understanding the behaviour of those model both from information-theoretic and computational point of view. This line of study brought up remarkable connections between physical phase transitions and appearance of computational hardness. A so-caller hard phase was identified where learning is possible, but no efficient algorithm are known to obtain it. This hard phase is located via a study of message passing algorithms.
In the existing literature, the hard phase is located using the simplest (replica symmetric) version of the message passing algorithms that ignores the fact that from the physics point of view this hard phase is glassy. Our contribution is the development of the approximate survey propagation (ASP) algorithm that takes glassines into account, in particular by breaking of the replica symmetry. We show that the large size limit of ASP algorithm leads to the one-step-replica symmetry breaking fixed-point equations well known from the context of spin glasses. Using this setting, we characterize the glassy property of the hard region, measuring the entropy of the metastable glassy states, called complexity. We show that this glassiness extends even outside of the hard phase thus strongly suggesting that sampling based algorithms such as Monte Carlo or Langevin sampling will not be able to match the performance of the simple message passing algorithms. This is contrary to what was widely believe in the field and is being confirmed using numerical simulations and analytical studies of the dynamics in simpler models.
Analyzing the ASP algorithm we reached another striking conclusion: ASP is unable to outperform the simpler message passing algorithm and so in particular ASP also does not work in the hard phase, this is despite taking correctly into account the glassiness while the simpler algorithm ignores it. This is a considerable evidence towards the fact that the hard phase is impenetrable for efficient algorithms for perhaps fundamental reasons, that are however ou of reach of current computational complexity theory. Further investigation of this point is an exciting direction both for physics and theoretical computer science.
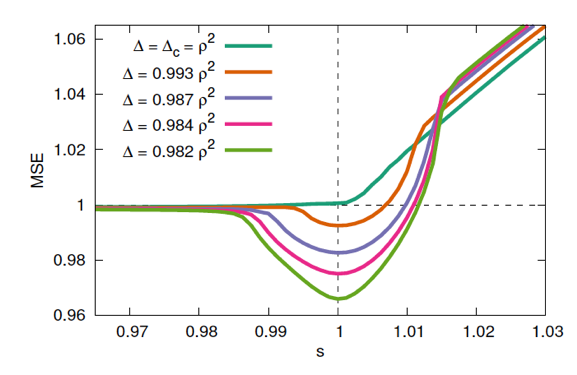
Mean Square Error of the ASP algorithm as a function of the Parisi parameter s on which the algorithm depends. We see that the minimal error is always reached for s=1 for which the ASP algorithm reduces to the simpler form that ignores glassy aspects of the hard phase.
F. Antenucci (CEA), P. Urbani (CEA), F. Krzakala (ENS), L. Zdeborová (CEA), Approximate Survey Propagation for Statistical Inference, Journal of Statistical Mechanics (2019)
F. Antenucci (CEA), S. Franz (LPTMS), P. Urbani (CEA), L. Zdeborová (CEA), On the glassy nature of the hard phase in inference problems, Phys. Rev. X 9, 011020 (2019)
Résultats obtenus dans le cadre du projet SaMURai financé par le thème émergence du LabEx PALM et porté par Lenka Zdeborová (CEA) et Silvio Franz (LPTMS)