V. Bouillaut, S. Lepot, B. Miquel, S. Aumaitre, B. Gallet (SPEC)
The heat flux transported by turbulent thermal convection has important implications for geophysical, astrophysical and industrial flows: one seeks a power-law relation Nu ∼ Raγ, where the Nusselt number Nu represents the dimensionless heat flux and the Rayleigh number Ra characterizes the internal temperature gradients. Decades of investigations of the Rayleigh-Bénard (RB) setup indicate that the heat transport is strongly restricted by boundary layers near the hot and cold solid plates. This prevents the observation of the “ultimate” scaling-regime of thermal convection, where bulk turbulence controls the convective heat flux independently of molecular viscosity and thermal diffusivity. This regime is characterized by a larger scaling exponent, γ = 0.5.In contrast to the RB setup, many geophysical and astrophysical convective flows are driven by radiation: absorption of incoming light by a body of fluid induces local heating. We have developed a laboratory experiment that reproduces such radiative heating: a mixture of water and dye contained inside a tank with transparent bottom plate absorbs an incoming upward flux of light. By changing the concentration of the dye, we can tune the thickness of the heating region. For large dye concentration, we heat up the fluid in the immediate vicinity of the bottom plate, in a similar fashion to the RB setup. By contrast, for low dye concentration we heat up the bulk turbulent flow directly, therefore bypassing the boundary layers. This allows us to continuously transition from the RB boundary-layer scaling to the ultimate scaling regime of turbulent convection [1,2]: the exponent γ increases from 0.3 for large dye concentration to 0.5 for low dye concentration. We have proposed a model for the heat transport in this novel radiatively driven convective flow. The model underlines the peculiar role of the Prandlt number (ratio of viscous diffusivity to thermal diffusivity), which we confirmed through an extensive study of the parameter space by means of state-of-the-art Direct Numerical Simulations [3].
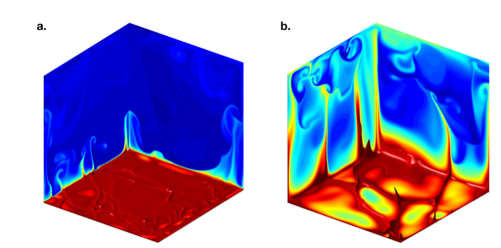
Snapshots of the temperature field from Direct Numerical Simulations. a. The absorption length is much smaller than the thermal boundary layer. The temperature gradients are located in the thermal boundary layer very near the bottom boundary, with narrow plumes seldom penetrating the bulk of the fluid domain. b. The absorption length is much larger than the thermal boundary layer: the region of warmfluid extends more in the verticaldirection, with taller and wider plumes penetrating the bulk turbulent region.
[1] S Lepot, S Aumaître, B Gallet, Proc Natl Acad Sci (2018) 115 (36) 8937-8941; DOI: https://doi.org/10.1073/pnas.1806823115
[2] V Bouillaut, S Lepot, S Aumaître, B Gallet, J. Fluid Mech. (2019), vol. 861, R5, doi:10.1017/jfm.2018.972 [3] B. Miquel, V Bouillaut, S Aumaître, B Gallet J. Fluid Mech. (2020), vol. 900, R1, DOI: https://doi.org/10.1017/jfm.2020.485
Results achieved in the framework of the project ConRad 2017 funded by topic 2 and carried out by Sébastien Aumaitre, Basile Gallet (SPEC) and Anne Davaille (FAST)